登山 補給站
專業戶外活動資訊平台
裝備討論區
探勘路線 - 簡易坡度計算

2008/4/1
坡度大於45度的地形, 除非綁上安全繩, 或有濃密樹枝可供攀爬, 或採之字繞行, 一般並不適合開成直線路. 但如何從地圖之等高線, 預先判斷某一條稜線或斜坡, 適不適合開路呢 ?
最簡單方法,是先計算出坡度值, 一般都用如下的簡單三角函數公式來算:
θ = TAN-1 (縱橫比) , ※ 縱橫比= 高度差/水平距離
譬如: 某地圖每方格為一公里長, 某一條稜通過此方格的總爬升高度:
1)=100公尺, 縱橫比=100/1000 = 0.1, 坡度為: TAN-1 (0.1) = 5.7°
2)=200公尺, 縱橫比=200/1000 = 0.2, 坡度為: TAN-1 (0.2) = 11.3°
3)=500公尺, 縱橫比=500/1000 = 0.5, 坡度為: TAN-1 (0.5) = 26.5°
4)=1000公尺,縱橫比=1000/1000= 1.0, 坡度為: TAN-1 (1.0) = 45°
5)=2000公尺,縱橫比=2000/1000= 2.0, 坡度為: TAN-1 (2.0) = 63°
但除非有計算機, 不然這個 TAN-1 函數是很難用的, 底下提供一個簡單估算法:
*** 坡度值 ~ 縱橫比 X 50 , 適用於縱橫比在 0~1 之間 *** :
1) 縱橫比= 0.1, 坡度 ~ 5 °
2) 縱橫比= 0.2, 坡度 ~ 10°
3) 縱橫比= 0.5, 坡度 ~ 25°
4) 縱橫比= 1.0, 坡度 ~ 50°
5) 縱橫比= 2.0, 坡度 ~ 100° (不適用, 誤差太大)
最好採用更小比例地圖, 譬如 1/10000 或 1/5000, 來估算更局部區域之縱橫比,以求坡度, 以免實際應用時, 在台灣這種常有極端地形變化的區域, 產生誤判.
建議新版地圖, 自動提供坡度量測工具 (本人獨創之新想法與專利, 凡採用之商業團體, 酌收營利之1% 費用, 最近很需要錢啊, 3Q)
最簡單方法,是先計算出坡度值, 一般都用如下的簡單三角函數公式來算:
θ = TAN-1 (縱橫比) , ※ 縱橫比= 高度差/水平距離
譬如: 某地圖每方格為一公里長, 某一條稜通過此方格的總爬升高度:
1)=100公尺, 縱橫比=100/1000 = 0.1, 坡度為: TAN-1 (0.1) = 5.7°
2)=200公尺, 縱橫比=200/1000 = 0.2, 坡度為: TAN-1 (0.2) = 11.3°
3)=500公尺, 縱橫比=500/1000 = 0.5, 坡度為: TAN-1 (0.5) = 26.5°
4)=1000公尺,縱橫比=1000/1000= 1.0, 坡度為: TAN-1 (1.0) = 45°
5)=2000公尺,縱橫比=2000/1000= 2.0, 坡度為: TAN-1 (2.0) = 63°
但除非有計算機, 不然這個 TAN-1 函數是很難用的, 底下提供一個簡單估算法:
*** 坡度值 ~ 縱橫比 X 50 , 適用於縱橫比在 0~1 之間 *** :
1) 縱橫比= 0.1, 坡度 ~ 5 °
2) 縱橫比= 0.2, 坡度 ~ 10°
3) 縱橫比= 0.5, 坡度 ~ 25°
4) 縱橫比= 1.0, 坡度 ~ 50°
5) 縱橫比= 2.0, 坡度 ~ 100° (不適用, 誤差太大)
最好採用更小比例地圖, 譬如 1/10000 或 1/5000, 來估算更局部區域之縱橫比,以求坡度, 以免實際應用時, 在台灣這種常有極端地形變化的區域, 產生誤判.
建議新版地圖, 自動提供坡度量測工具 (本人獨創之新想法與專利, 凡採用之商業團體, 酌收營利之1% 費用, 最近很需要錢啊, 3Q)
文章附件
所有回覆
-
 我也一樣, 最近也很需要錢. 您那台 250機車賣掉沒, 花蓮 aego 兄不是想買一台越野機車. 若還沒賣掉, 你們可 talk talk.
我也一樣, 最近也很需要錢. 您那台 250機車賣掉沒, 花蓮 aego 兄不是想買一台越野機車. 若還沒賣掉, 你們可 talk talk. -
 >>但如何從地圖之等高線, 預先判斷某一條稜線或斜坡, 適不適合開路呢 ? 老實說, 單純這樣是沒辦法判斷的, 因為 1.事在人為 2.局部化地形 3.之字坡可化解 4.當地植被 5.當地土石狀況 不過後面的就比較有意思... { [獨創] 鄒仔山林穿越之坡度與時間速算方式 http://www.keepon.com.tw/ActiveSite/Message/One.asp?MessageID=66646&Process=Group } 另外舊版地圖有坡度尺, 新版的不提供, 自己也可透過長度就算出來了, 你這樣還要除來除去再對表太累了. 而且最重要一點, 在實戰經驗中, 這Mapsoure的TOPO不合啦, 用1/25000之一的卡實在, 用等高首曲線卡實在, 也不用再那邊換成 實際長度, 多那麼多步驟. 如果有帶手機, 要算這真實坡度的精準很容易, 但求非常精準是要幹麻? 我不知道? 至於我的版權說明, 就如那連結所言, 至於使用,全部免費, 我們標榜 Simpe! Easy! Safe! Happy! Funny! 甚至是 Free! 和 [貝戈戈]TM, [狗皮膏]TM. Enjoy it!
>>但如何從地圖之等高線, 預先判斷某一條稜線或斜坡, 適不適合開路呢 ? 老實說, 單純這樣是沒辦法判斷的, 因為 1.事在人為 2.局部化地形 3.之字坡可化解 4.當地植被 5.當地土石狀況 不過後面的就比較有意思... { [獨創] 鄒仔山林穿越之坡度與時間速算方式 http://www.keepon.com.tw/ActiveSite/Message/One.asp?MessageID=66646&Process=Group } 另外舊版地圖有坡度尺, 新版的不提供, 自己也可透過長度就算出來了, 你這樣還要除來除去再對表太累了. 而且最重要一點, 在實戰經驗中, 這Mapsoure的TOPO不合啦, 用1/25000之一的卡實在, 用等高首曲線卡實在, 也不用再那邊換成 實際長度, 多那麼多步驟. 如果有帶手機, 要算這真實坡度的精準很容易, 但求非常精準是要幹麻? 我不知道? 至於我的版權說明, 就如那連結所言, 至於使用,全部免費, 我們標榜 Simpe! Easy! Safe! Happy! Funny! 甚至是 Free! 和 [貝戈戈]TM, [狗皮膏]TM. Enjoy it! -
 鄒仔,你那個太難, 要開根號, 要算爬升時間, 而且是[事後算]... 我這個只要拿森林指北針量一量地圖距離, 用簡單心算求縱橫比, 再乘以50, 就很準囉, 而且是[事前算]喔, 呵呵. 註: [事前算] 是為了決定開哪一條路, 以免開了一半才後悔. Hunter, 那台車嚇嚇叫, 騎的很爽哩, 賣 ? , 可以呀, 一句話 , 免談.
鄒仔,你那個太難, 要開根號, 要算爬升時間, 而且是[事後算]... 我這個只要拿森林指北針量一量地圖距離, 用簡單心算求縱橫比, 再乘以50, 就很準囉, 而且是[事前算]喔, 呵呵. 註: [事前算] 是為了決定開哪一條路, 以免開了一半才後悔. Hunter, 那台車嚇嚇叫, 騎的很爽哩, 賣 ? , 可以呀, 一句話 , 免談. -
 不用功, 扣分. 等高線坡度還會跟人為的方格走, 你是自欺欺人喔. 當然我們都是紙上談兵, 先作功課, 大方向確定, 最後還不是要回到現實, 附上山徑就是讓大家了解, 最後都會根據實際情形修正的, 包含您的起登點都是錯的! 一條直線? 用來推估? 算了吧?! 高角度而不為? 算了吧! 卡在中間進退不得也得行動...橫渡吧! 高繞? 沒聽過低繞? 轉進也是一種作為. 還是用GPS直線導航, 不斷推進, 不斷修正方向, 才是可行的. 不然...不要開路啦! 夠用就好.
不用功, 扣分. 等高線坡度還會跟人為的方格走, 你是自欺欺人喔. 當然我們都是紙上談兵, 先作功課, 大方向確定, 最後還不是要回到現實, 附上山徑就是讓大家了解, 最後都會根據實際情形修正的, 包含您的起登點都是錯的! 一條直線? 用來推估? 算了吧?! 高角度而不為? 算了吧! 卡在中間進退不得也得行動...橫渡吧! 高繞? 沒聽過低繞? 轉進也是一種作為. 還是用GPS直線導航, 不斷推進, 不斷修正方向, 才是可行的. 不然...不要開路啦! 夠用就好. -
 呵呵, 我是舉例, 別吹毛求疵啦, 看的懂的, 應該會了解我是想表達垂直或水平於方格線的稜線為例.
呵呵, 我是舉例, 別吹毛求疵啦, 看的懂的, 應該會了解我是想表達垂直或水平於方格線的稜線為例. -
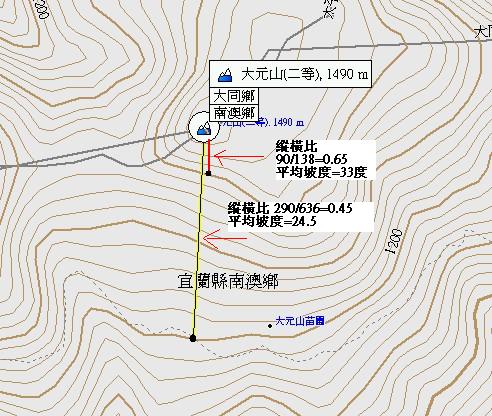
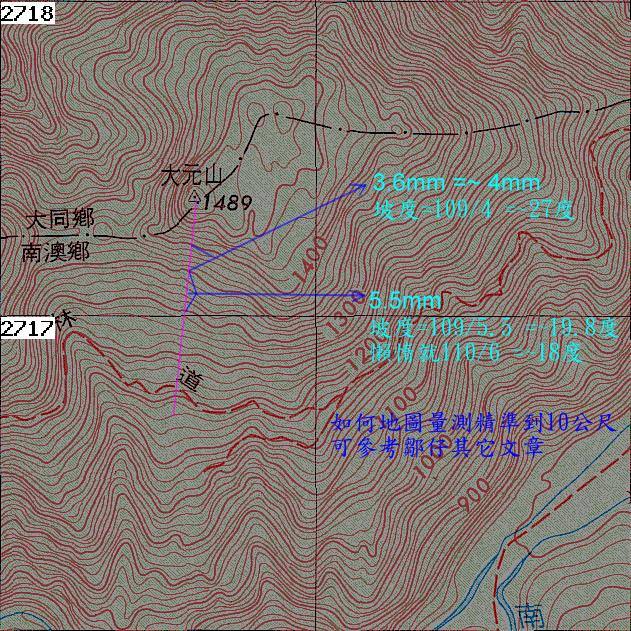
 其實您的方法就是我說的方法, 原理都是一樣的......(應該很多人不會去探究) 以大元山為例, 量出首曲線(有人採用其它名詞,就是兩粗線通過的直線)之地圖長度. *上面較陡之一小段 3.6mm =~ 4mm 坡度=109/4 =~27度 *下面較緩之一小段 5.5mm 坡度=109/5.5 =~19.8度 懶惰就110/6 =~18度 這樣是不是也不難? 更不需要再換算[實距], 直接用[圖距]就完成了. 而且您可以發現, 單單這兩段等高線就有20和27度的差距, 而實際若一定要照圖面規劃推進, 也必須不斷修正, 比用長距離的平均坡度更佳. 至於, 如何地圖量測精準到10公尺? 圖距和實距的轉換, 可參考鄒仔其它文章. 鄒仔的坡度算法可以不須要到此進階的概念. { [獨創] 鄒仔山林穿越之坡度與時間速算方式 http://www.keepon.com.tw/ActiveSite/Message/One.asp?MessageID=66646 [考題] 如何讓傳統判圖之量測精準度大於雞屁ㄟ屎的精準度? http://www.keepon.com.tw/ActiveSite/Message/One.asp?MessageID=66734 } ps.至於109之數字如何而來, 我是實驗統計過算出來的, 不然用110不是更方便計算?
其實您的方法就是我說的方法, 原理都是一樣的......(應該很多人不會去探究) 以大元山為例, 量出首曲線(有人採用其它名詞,就是兩粗線通過的直線)之地圖長度. *上面較陡之一小段 3.6mm =~ 4mm 坡度=109/4 =~27度 *下面較緩之一小段 5.5mm 坡度=109/5.5 =~19.8度 懶惰就110/6 =~18度 這樣是不是也不難? 更不需要再換算[實距], 直接用[圖距]就完成了. 而且您可以發現, 單單這兩段等高線就有20和27度的差距, 而實際若一定要照圖面規劃推進, 也必須不斷修正, 比用長距離的平均坡度更佳. 至於, 如何地圖量測精準到10公尺? 圖距和實距的轉換, 可參考鄒仔其它文章. 鄒仔的坡度算法可以不須要到此進階的概念. { [獨創] 鄒仔山林穿越之坡度與時間速算方式 http://www.keepon.com.tw/ActiveSite/Message/One.asp?MessageID=66646 [考題] 如何讓傳統判圖之量測精準度大於雞屁ㄟ屎的精準度? http://www.keepon.com.tw/ActiveSite/Message/One.asp?MessageID=66734 } ps.至於109之數字如何而來, 我是實驗統計過算出來的, 不然用110不是更方便計算? -
 哈, 我果然不用功, 計算時間與坡度, 原來是兩件事哩. 我大概看懂你的算法, 但坡度與時間一起處理, 剛看就覺得複雜, 要記口訣, 要記數字...感覺太難.. 如果不算時間, 或兩者分開寫, 也許感覺簡單些.
哈, 我果然不用功, 計算時間與坡度, 原來是兩件事哩. 我大概看懂你的算法, 但坡度與時間一起處理, 剛看就覺得複雜, 要記口訣, 要記數字...感覺太難.. 如果不算時間, 或兩者分開寫, 也許感覺簡單些. -
 其實我也該檢討, 只是有時想, 如果有趣的寶藏是大家都可以碰到的, 那應該就不是寶藏了, 只好給有興趣的人去發現, 是故, 就給它丟在那邊. 而最重要的是, 寶藏就是看過後, 學習消化過後, 才算是自己的, 但我通常研究過後, 自己也忘了......所以才要留下一些隻字片語. 至於為何要記? 因為什麼額外的道具都沒帶才是最simple最easy的. 若以前兩段之sample, 先20度再27度. 時間算法就是 費時分鐘 = 35 / 度數@五指兄弟的順序 [[[ 1(大姆哥)-3(食指)-7(中指)-11(無名指)-21(小指) ]]] 20度落在(無名指), 也就是第四指, 故 費時 = 35 / 4 = 8.75, 約9分鐘. 27度落在(小指), 也就是第五指, 故 費時 = 35 / 5 = 7, 約7分鐘. 此兩段爬升總共需費時 9+7=16分鐘. 當然前提是在既有開闢良好之山徑, 而超過10度以上或狀況不佳之中級山, 建議採用49替代35, 也就是時間會增長. 49/4 + 49/5 = 12.25 + 9.8 = 22.05 分鐘 時間會由16分鐘增長到22分鐘, 增加約6分鐘, 而這六分鐘, 剛好可以護一生呢, 不!不! 是在整個山行過程中, 只是一個微小的因子.
其實我也該檢討, 只是有時想, 如果有趣的寶藏是大家都可以碰到的, 那應該就不是寶藏了, 只好給有興趣的人去發現, 是故, 就給它丟在那邊. 而最重要的是, 寶藏就是看過後, 學習消化過後, 才算是自己的, 但我通常研究過後, 自己也忘了......所以才要留下一些隻字片語. 至於為何要記? 因為什麼額外的道具都沒帶才是最simple最easy的. 若以前兩段之sample, 先20度再27度. 時間算法就是 費時分鐘 = 35 / 度數@五指兄弟的順序 [[[ 1(大姆哥)-3(食指)-7(中指)-11(無名指)-21(小指) ]]] 20度落在(無名指), 也就是第四指, 故 費時 = 35 / 4 = 8.75, 約9分鐘. 27度落在(小指), 也就是第五指, 故 費時 = 35 / 5 = 7, 約7分鐘. 此兩段爬升總共需費時 9+7=16分鐘. 當然前提是在既有開闢良好之山徑, 而超過10度以上或狀況不佳之中級山, 建議採用49替代35, 也就是時間會增長. 49/4 + 49/5 = 12.25 + 9.8 = 22.05 分鐘 時間會由16分鐘增長到22分鐘, 增加約6分鐘, 而這六分鐘, 剛好可以護一生呢, 不!不! 是在整個山行過程中, 只是一個微小的因子. -
 如果 109 這經驗值夠準的話, 其他非1/25000 地圖, 應該可以使用等比例的經驗轉移值(Trim Factor,TF) 來計算: 1/25000 -> 109 1/10000 -> 109 * 2.5 = 272.5 ※TF=25000/10000=2.5 1/5000 -> 109 * 5 = 545 ※TF=25000/5000 =5 或公式改為: 坡度 = [109 / 圖距] * TF ※ TF= 25000 /地圖比例 以 1/5000地圖, 測量圖距=25mm 為例: 坡度 = [109 / 25] * [25000/5000] = 21.8度. 不知這樣計算可行嗎 ?
如果 109 這經驗值夠準的話, 其他非1/25000 地圖, 應該可以使用等比例的經驗轉移值(Trim Factor,TF) 來計算: 1/25000 -> 109 1/10000 -> 109 * 2.5 = 272.5 ※TF=25000/10000=2.5 1/5000 -> 109 * 5 = 545 ※TF=25000/5000 =5 或公式改為: 坡度 = [109 / 圖距] * TF ※ TF= 25000 /地圖比例 以 1/5000地圖, 測量圖距=25mm 為例: 坡度 = [109 / 25] * [25000/5000] = 21.8度. 不知這樣計算可行嗎 ? -
 轉移問題, 留給您或有興趣的人研究, 因為我不想一個頭兩個大, 不過確實我之前有套用過, 至於結果如何? 忘了?
轉移問題, 留給您或有興趣的人研究, 因為我不想一個頭兩個大, 不過確實我之前有套用過, 至於結果如何? 忘了? -
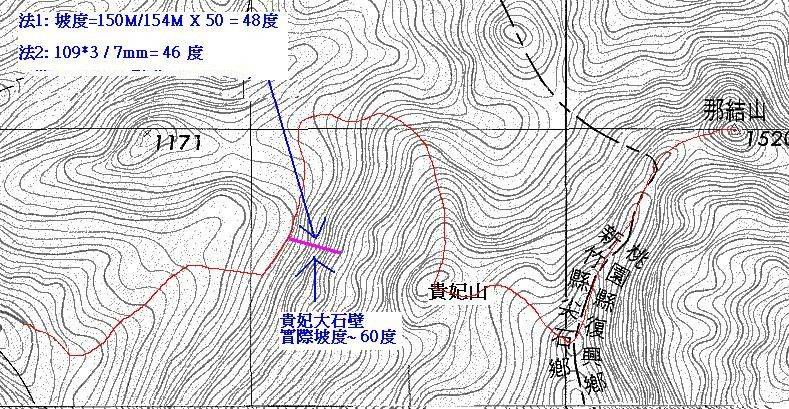
 新竹最有名的大石壁 - 貴妃石壁 或貴妃屏, 其實際坡度約為60~65度. 底下以 Smile 及 鄒仔的方法來紙上預測, 請參考附圖 1/25000 1) 取三條等高圖主線,落差 = 150M, 圖距=7mm. 2) 每方格4.55cm=1公里,不是正確的 4cm, 故1mm = 22 公尺 => 7mm = 154 公尺. Smile 法: 坡度 = 縱橫比 * 50 = 150公尺 / 154公尺 * 50 = 48 度 鄒法 : 坡度 = 109 * 3 / 7 mm = 46 度 (有三格故乘以3) (因地圖比例誤差,故更正: 坡度 = 109 * 3 / (7 mm * 4/ 4.55) = 53 度 與實際60度有差距, 此為地圖準確度不夠所致. 貴妃石壁, 實際坡度照片, 先參考 (今晚補圖) => http://www.keepon.com.tw/ActiveSite/Article/One.asp?ArticleID=17572
新竹最有名的大石壁 - 貴妃石壁 或貴妃屏, 其實際坡度約為60~65度. 底下以 Smile 及 鄒仔的方法來紙上預測, 請參考附圖 1/25000 1) 取三條等高圖主線,落差 = 150M, 圖距=7mm. 2) 每方格4.55cm=1公里,不是正確的 4cm, 故1mm = 22 公尺 => 7mm = 154 公尺. Smile 法: 坡度 = 縱橫比 * 50 = 150公尺 / 154公尺 * 50 = 48 度 鄒法 : 坡度 = 109 * 3 / 7 mm = 46 度 (有三格故乘以3) (因地圖比例誤差,故更正: 坡度 = 109 * 3 / (7 mm * 4/ 4.55) = 53 度 與實際60度有差距, 此為地圖準確度不夠所致. 貴妃石壁, 實際坡度照片, 先參考 (今晚補圖) => http://www.keepon.com.tw/ActiveSite/Article/One.asp?ArticleID=17572 -
 >>2) 每方格1公里=4.55cm,不是正確的 5cm, 故1mm = 22 公尺 => 7mm = 154 公尺. 是40mm啦! >>Smile 法: 坡度 = 縱橫比 * 50 = 150公尺 / 154公尺 * 50 = 48 度 >>鄒法 : 坡度 = 109 * 3 / 7 mm = 46 度 (有三格故乘以3) 您算錯了! 既然是您的方格不準, 那換算後7mm應該會變小. (7/45.5)*40=6.1538461538461538461538461538462 6.1538461538461538461538461538462/3=~2.05 109/2.05=53.17
>>2) 每方格1公里=4.55cm,不是正確的 5cm, 故1mm = 22 公尺 => 7mm = 154 公尺. 是40mm啦! >>Smile 法: 坡度 = 縱橫比 * 50 = 150公尺 / 154公尺 * 50 = 48 度 >>鄒法 : 坡度 = 109 * 3 / 7 mm = 46 度 (有三格故乘以3) 您算錯了! 既然是您的方格不準, 那換算後7mm應該會變小. (7/45.5)*40=6.1538461538461538461538461538462 6.1538461538461538461538461538462/3=~2.05 109/2.05=53.17 -
 我知道是40mm , 不是50mm, 想吃午飯完,再回來修改,但你的回應太快了, 我都還沒修正哩. 如果你那109是在1/25000, 方格40mm 下得到的, 這樣重算是對的. 不過建議你還是先確認一下, 得到109時, 你那方格真的是 40mm 嗎 ?
我知道是40mm , 不是50mm, 想吃午飯完,再回來修改,但你的回應太快了, 我都還沒修正哩. 如果你那109是在1/25000, 方格40mm 下得到的, 這樣重算是對的. 不過建議你還是先確認一下, 得到109時, 你那方格真的是 40mm 嗎 ? -
 還是用我那招 [[[城市跑兩點]]] ↓↑ [[[兩顆蛋廚司]]] ↓:實距轉圖距 ↑:圖距轉實距 您的資料換算後為 實距:153.84m =~ 154m 圖距:154*4=616→6.16 換算後首曲線為2mm 故 109/2=54.5度 基本上我也忘了當初我是取到那些範圍的最佳值. 您的乘50在我的規則中就是把109換成100霸了, 不要傷腦筋了, 鄒仔的方法已經把一些東西去蕪存菁了, 就相信我這一次, 除非您找到比109更好的數字, 其實在不同區段也有找到110等其他更適合的, 不過為了折衷登山的狀況, 就取用109之參數. 就如您說的應該是60度, 您的方式不過是會把角度算得更低, 當然如果您量圖距夠精準, 那麼109改成120就剛剛好, 當然假設我這模型是OK的, 那麼您的圖距應該量出 1.8166666666666666666666666666667 三倍後剛好5.45mm(但您的尺無法量出這樣的數據, 鄒仔已經提供一展明燈了...) 而若要到這般的精準, 您可以參考另一篇精準到10m的文章技巧, 那是精準到0.4mm圖距的方法, 智慧存在已久, 用在登山領域絕對是鄒仔獨創的, 只是怕有人不了解原理, 這10m精準夠了, 雖然可以達到0.01mm(精準到實距25cm), 但是地圖的誤差(我研究過論文驗證過了)遠高過這個數值. 我再更深入(應該沒幾個人看得懂?), 以10m精準對應到圖距為0.4mm狀況 (20.185185185185185185185185185185-18.793103448275862068965517241379)*3=4.17624521072796934865900383143 也就是在只能精準到10m級的地圖(包含量測)來回差異會有4度的誤差, 甚至會產生近8度的狀況. 而如果您只能辨識0.5mm 會達到5~6度的狀況, 甚至是12度的誤差. 也就是說, 以目前的量測狀況, 微笑兄, 不要太傷心, 您算出來的48度, 加上這12度就是幾乎正確了, 當然如果減個12度就差很多了. (其實應該是48+-6才對 42~54度.) ps.我的理論依據不是實況, 是數學算出來的, 其實用excel三角函數就可以推導了.
還是用我那招 [[[城市跑兩點]]] ↓↑ [[[兩顆蛋廚司]]] ↓:實距轉圖距 ↑:圖距轉實距 您的資料換算後為 實距:153.84m =~ 154m 圖距:154*4=616→6.16 換算後首曲線為2mm 故 109/2=54.5度 基本上我也忘了當初我是取到那些範圍的最佳值. 您的乘50在我的規則中就是把109換成100霸了, 不要傷腦筋了, 鄒仔的方法已經把一些東西去蕪存菁了, 就相信我這一次, 除非您找到比109更好的數字, 其實在不同區段也有找到110等其他更適合的, 不過為了折衷登山的狀況, 就取用109之參數. 就如您說的應該是60度, 您的方式不過是會把角度算得更低, 當然如果您量圖距夠精準, 那麼109改成120就剛剛好, 當然假設我這模型是OK的, 那麼您的圖距應該量出 1.8166666666666666666666666666667 三倍後剛好5.45mm(但您的尺無法量出這樣的數據, 鄒仔已經提供一展明燈了...) 而若要到這般的精準, 您可以參考另一篇精準到10m的文章技巧, 那是精準到0.4mm圖距的方法, 智慧存在已久, 用在登山領域絕對是鄒仔獨創的, 只是怕有人不了解原理, 這10m精準夠了, 雖然可以達到0.01mm(精準到實距25cm), 但是地圖的誤差(我研究過論文驗證過了)遠高過這個數值. 我再更深入(應該沒幾個人看得懂?), 以10m精準對應到圖距為0.4mm狀況 (20.185185185185185185185185185185-18.793103448275862068965517241379)*3=4.17624521072796934865900383143 也就是在只能精準到10m級的地圖(包含量測)來回差異會有4度的誤差, 甚至會產生近8度的狀況. 而如果您只能辨識0.5mm 會達到5~6度的狀況, 甚至是12度的誤差. 也就是說, 以目前的量測狀況, 微笑兄, 不要太傷心, 您算出來的48度, 加上這12度就是幾乎正確了, 當然如果減個12度就差很多了. (其實應該是48+-6才對 42~54度.) ps.我的理論依據不是實況, 是數學算出來的, 其實用excel三角函數就可以推導了. -
 >>如果你那109是在1/25000, 方格40mm 下得到的, 這樣重算是對的. 不過建議 >>你還是先確認一下, 得到109時, 你那方格真的是 40mm 嗎 ? 再重覆一次 我的理論依據, 不是經驗, 是數學推導的, 故沒有方格實際大小的問題啦! 如果您要我舉出實證, 沒錯, 我手邊也有"真港"的官方地圖, 就是40mm, 這個方式比那個早期官方的內建坡度表來的有智慧, 請不要這樣污辱我! 哇哈哈! 我也有用蚯蚓的地圖產生器, 不過我都用電腦內建的軟體印出來, 也不會像你差那麼多, 不過多個2ㄇㄞㄇㄞ(2mm). 不過您也太強了吧? 要我看, 我都不曉得坡或壁有幾度? 你不會偷拿水準儀之類的去偷量角度吧? 這讓想到一位科學家的故事, 我在青少年時期聽到, 就深深吸引著我, 某位科學家到郊外欣賞美麗的瀑布, 把雨傘頂端拿開, 深入瀑布水中量溫度, 得知瀑布下面的水比瀑布上面的水溫高, 因為水在下降過程摩擦生熱. 太屌了! 隨手都有傢私.
>>如果你那109是在1/25000, 方格40mm 下得到的, 這樣重算是對的. 不過建議 >>你還是先確認一下, 得到109時, 你那方格真的是 40mm 嗎 ? 再重覆一次 我的理論依據, 不是經驗, 是數學推導的, 故沒有方格實際大小的問題啦! 如果您要我舉出實證, 沒錯, 我手邊也有"真港"的官方地圖, 就是40mm, 這個方式比那個早期官方的內建坡度表來的有智慧, 請不要這樣污辱我! 哇哈哈! 我也有用蚯蚓的地圖產生器, 不過我都用電腦內建的軟體印出來, 也不會像你差那麼多, 不過多個2ㄇㄞㄇㄞ(2mm). 不過您也太強了吧? 要我看, 我都不曉得坡或壁有幾度? 你不會偷拿水準儀之類的去偷量角度吧? 這讓想到一位科學家的故事, 我在青少年時期聽到, 就深深吸引著我, 某位科學家到郊外欣賞美麗的瀑布, 把雨傘頂端拿開, 深入瀑布水中量溫度, 得知瀑布下面的水比瀑布上面的水溫高, 因為水在下降過程摩擦生熱. 太屌了! 隨手都有傢私. -
 >> 我的理論依據, 不是經驗, 是數學推導的, 故沒有方格實際大小的問題啦! 蚯蚓那個,以一般軟體,不調比例下,印出來,會在42~46 mm 間, 不會是40mm, 這個誤差, 再套你那個109時, 若不注意, 就差很多. 也就是必須正好方格=40mm, 比例為1/25000,並限定為經建版的地圖, 因不同繪圖公司之等高圖,其坡度與水平距離關係, 不見得會採用線性,故"實驗統計值" 109,不見得可用 (本來想寫"經驗值", 但鄒仔這麼在意, 就收回囉). 固定垂直高度下(Y), 坡度(Angle) 與水平距離(X) 變化關係, 不會是線性的, 除非地圖公司, 故意用線性方式來畫等高圖. 若以三角函數關係來畫等高圖, 設定高度主線間距為50M 時: 1) 設定 X=1mm, 坡度=60度, 得Y=√3 mm (代表 50M 高, 並固定此值) 2) 故若 X=2mm, 坡度=40.89度 3) 故若 X=3mm, 坡度=29.99度 4) 故若 X=4mm, 坡度=23.41度 得坡度 與 X 關係為: Angle = 69 / X^-0.83 , 不是線性的, 故此類等高圖, 不能用69 直接除以 X.
>> 我的理論依據, 不是經驗, 是數學推導的, 故沒有方格實際大小的問題啦! 蚯蚓那個,以一般軟體,不調比例下,印出來,會在42~46 mm 間, 不會是40mm, 這個誤差, 再套你那個109時, 若不注意, 就差很多. 也就是必須正好方格=40mm, 比例為1/25000,並限定為經建版的地圖, 因不同繪圖公司之等高圖,其坡度與水平距離關係, 不見得會採用線性,故"實驗統計值" 109,不見得可用 (本來想寫"經驗值", 但鄒仔這麼在意, 就收回囉). 固定垂直高度下(Y), 坡度(Angle) 與水平距離(X) 變化關係, 不會是線性的, 除非地圖公司, 故意用線性方式來畫等高圖. 若以三角函數關係來畫等高圖, 設定高度主線間距為50M 時: 1) 設定 X=1mm, 坡度=60度, 得Y=√3 mm (代表 50M 高, 並固定此值) 2) 故若 X=2mm, 坡度=40.89度 3) 故若 X=3mm, 坡度=29.99度 4) 故若 X=4mm, 坡度=23.41度 得坡度 與 X 關係為: Angle = 69 / X^-0.83 , 不是線性的, 故此類等高圖, 不能用69 直接除以 X. -
 當然! 我們的都是"速算"(相對於精算), 就是為了偷懶和方便, 如果是線性的, 世上就不會有三角函數的出現了. 還有正規的坡度表沒有高角度的. 45度以上歸類於峭壁, 參相關討論 http://www.keepon.com.tw/ActiveSite/Message/One.asp?MessageID=66594 坡度表製作原理 ───────────────────────────── 時間為分:秒, 水平圖差單位為mm, 坡度1~4度可採用計曲線, 長度如括弧內. ───────────────────────────── 時間 48:58 27:28 20:18 16:43 14:34 13:8 12:6 11:20 10:44 10:15 水平圖差 114.6 57.3 38.2 28.6 22.9 19.0 16.3 14.2 12.6 11.3 坡度 1 2 3 4 5 6 7 8 9 10 (22.9 11.5 7.6 5.7) 時間 9:51 9:31 9:14 9:0 8:47 8:36 8:27 8:18 8:10 8:3 水平圖差 10.3 9.4 8.7 8.0 7.5 7.0 6.5 6.2 5.8 5.5 坡度 11 12 13 14 15 16 17 18 19 20 時間 7:57 7:51 7:46 7:41 7:36 7:32 7:28 7:24 7:21 7:17 水平圖差 5.2 5.0 4.7 4.5 4.3 4.1 3.9 3.8 3.6 3.5 坡度 21 22 23 24 25 26 27 28 29 30 ───────────────────────────── 比對值之差異 http://www.keepon.com.tw/UploadFile/Message/2008/2/{2D1A9998-245B-4D1D-A6B1-83E2C5847C75}.jpg
當然! 我們的都是"速算"(相對於精算), 就是為了偷懶和方便, 如果是線性的, 世上就不會有三角函數的出現了. 還有正規的坡度表沒有高角度的. 45度以上歸類於峭壁, 參相關討論 http://www.keepon.com.tw/ActiveSite/Message/One.asp?MessageID=66594 坡度表製作原理 ───────────────────────────── 時間為分:秒, 水平圖差單位為mm, 坡度1~4度可採用計曲線, 長度如括弧內. ───────────────────────────── 時間 48:58 27:28 20:18 16:43 14:34 13:8 12:6 11:20 10:44 10:15 水平圖差 114.6 57.3 38.2 28.6 22.9 19.0 16.3 14.2 12.6 11.3 坡度 1 2 3 4 5 6 7 8 9 10 (22.9 11.5 7.6 5.7) 時間 9:51 9:31 9:14 9:0 8:47 8:36 8:27 8:18 8:10 8:3 水平圖差 10.3 9.4 8.7 8.0 7.5 7.0 6.5 6.2 5.8 5.5 坡度 11 12 13 14 15 16 17 18 19 20 時間 7:57 7:51 7:46 7:41 7:36 7:32 7:28 7:24 7:21 7:17 水平圖差 5.2 5.0 4.7 4.5 4.3 4.1 3.9 3.8 3.6 3.5 坡度 21 22 23 24 25 26 27 28 29 30 ───────────────────────────── 比對值之差異 http://www.keepon.com.tw/UploadFile/Message/2008/2/{2D1A9998-245B-4D1D-A6B1-83E2C5847C75}.jpg -
 還有您算的資料跟我不太一樣. 圖距(mm) 坡度(角度) 1 63.43 2 45.00 3 33.69 4 26.57 5 21.80 6 18.43 7 15.95 8 14.04 9 12.53 10 11.31 11 10.30 12 9.46 13 8.75 14 8.13 15 7.59 16 7.13 17 6.71 18 6.34 19 6.01 20 5.71 21 5.44 22 5.19 23 4.97 24 4.76 25 4.57 26 4.40 27 4.24 28 4.09 29 3.95 30 3.81 31 3.69 32 3.58 33 3.47 34 3.37 35 3.27 36 3.18 37 3.09 38 3.01 39 2.94 40 2.86 一方格到40mm, 是故到此. 回到您當初的歸納與結論, 超過45度開路算有點難度(不適合), !!!所以也就是兩首曲線間小於2mm就不適合開路.!!! !!!若以一般之30度以內, 那麼就是3.8mm左右,!!! !!!約略是4mm(坡度28~29度左右).!!! 這樣是不是更容易理解? 更simple更easy?
還有您算的資料跟我不太一樣. 圖距(mm) 坡度(角度) 1 63.43 2 45.00 3 33.69 4 26.57 5 21.80 6 18.43 7 15.95 8 14.04 9 12.53 10 11.31 11 10.30 12 9.46 13 8.75 14 8.13 15 7.59 16 7.13 17 6.71 18 6.34 19 6.01 20 5.71 21 5.44 22 5.19 23 4.97 24 4.76 25 4.57 26 4.40 27 4.24 28 4.09 29 3.95 30 3.81 31 3.69 32 3.58 33 3.47 34 3.37 35 3.27 36 3.18 37 3.09 38 3.01 39 2.94 40 2.86 一方格到40mm, 是故到此. 回到您當初的歸納與結論, 超過45度開路算有點難度(不適合), !!!所以也就是兩首曲線間小於2mm就不適合開路.!!! !!!若以一般之30度以內, 那麼就是3.8mm左右,!!! !!!約略是4mm(坡度28~29度左右).!!! 這樣是不是更容易理解? 更simple更easy? -
 我們學理工的(是嗎? 我是亂學一通!)有時候就是很想研究, 自然界是否有公式, 或許目前沒有, 未來會出現? 不過世界充滿變化, 太難掌握, 研究這些也算是額外的樂趣, 相關的文章(疑! 您也有參與討論...) 為何爬山走之字形較好?科學研究:較不會喘 http://www.keepon.com.tw/ActiveSite/Article/One.asp?ArticleID=22879 其中的 攀爬理論很難套用在實際山野 (A mathematical theory of climbing) 不過那篇文章似乎就是針對攀岩了. ps.之字坡 (zig-zag or traverse)
我們學理工的(是嗎? 我是亂學一通!)有時候就是很想研究, 自然界是否有公式, 或許目前沒有, 未來會出現? 不過世界充滿變化, 太難掌握, 研究這些也算是額外的樂趣, 相關的文章(疑! 您也有參與討論...) 為何爬山走之字形較好?科學研究:較不會喘 http://www.keepon.com.tw/ActiveSite/Article/One.asp?ArticleID=22879 其中的 攀爬理論很難套用在實際山野 (A mathematical theory of climbing) 不過那篇文章似乎就是針對攀岩了. ps.之字坡 (zig-zag or traverse) -
 貴妃大石壁照片來啦, 底部角度約為52度, 看來似乎是鄒仔的公式比較準喔.(但使用時,要注意是否需校正方格Size 誤差). 現場整體看,角度約60左右. 任何攀岩高手, 能從貴妃石壁, 直接爬上貴妃山頂, 本人提供至少值3000元的全新登山用品, 做為獎勵. 限三名. http://www.keepon.com.tw/ActiveSite/Article/One.asp?ArticleID=23378
貴妃大石壁照片來啦, 底部角度約為52度, 看來似乎是鄒仔的公式比較準喔.(但使用時,要注意是否需校正方格Size 誤差). 現場整體看,角度約60左右. 任何攀岩高手, 能從貴妃石壁, 直接爬上貴妃山頂, 本人提供至少值3000元的全新登山用品, 做為獎勵. 限三名. http://www.keepon.com.tw/ActiveSite/Article/One.asp?ArticleID=23378